Pattern Formation and Waves (1)
Traveling waves: The existence of traveling waves were shown
both analytically and numerically in various situations and for
different models in various applications. These include collaborations
with P. Carter & B. Sandstede (Brown University, USA), Y. Gaididei
(Kiev, Ukraine), R. Berkemer (DTU), P. L. Christiansen,
M.P. Sørensen (DTU), J.J. Rasmussen (DTU), A. Kawamoto &
T. Shiga (Toyota CRDL, Japan), M. Eiswirth, H. Rotermund, G. Ertl
(Frith Haber Institut, Berlin). For details see Journal of Evolution
Equations and Control Theory (EECT) 8(1), 73-100, 2019;
SIAM Journal on Applied Mathematics 74(6),
1895-1918, 2014;
NHM (Networks and Heterogeneous Media) 8(1), 261-273, 2013;
New Journal of Physics 11, 073012, 2009;
Europhysics Letters 73 (6), 820 - 825, 2006.
(2) Pattern formation principles to control cooperative robots:
Pattern formation principles were used to construct a
self-organized control for distributed robots and flexible
manufacturing sytems. It can be proven that only feasible solutions of
the underlying combinatorial optimziation problem emerge from the
pattern formation principle. This is in parts joint work with
C. Ellsaesser, University of Heidelberg, T. Fukuda (Nagoya University),
H. Haken (University of Stuttgart), P. Molnar (Clark Atlanta University)
and M. Schanz (University of Stuttgart). For details see e.g.
Physics Letters A 375, 2094 - 2098, 2011;
The International Journal of Robotics Research 24,
465 - 486, 2005;
IEEE Transactions on
Systems, Men and Cybernetics: Part B, 31, No. 3, 433 - 436,
2001.
(3) Pattern formation in many-particle systems:
It is proven that a interacting many-particle system of different
particle types with attracting interactions between particles of the
same type and repulsive interactions between particles of different
type converges under certain assumption to a sorted state. This is
joint work with S. Kokkendorff (DTU), J. Strotmann (University of
Hohenheim), N. Hummel (University of Heidelberg). For details see SIAM
Journal on Applied Mathematics (SIAP) 70(7), 2534 - 2555,
2010.
Deterministic and Stochastic Modelling Stochastic
many-particle systems have been formulated and
investigated. Construction of a mesoscopic stochastic lattice model
for fast simulations of large particle numbers for systems with local
mixing by diffusion. Fluctuation induced pattern formation was
investigated. Limit equations of stochastic many particle systems were
rigorously derived. This is joint work with M. Eiswirth,
H. Rotermund, G. Ertl (Frith Haber Institut, Berlin), K. Oelschlaeger
(University of Heidelberg) and C. Reichert (University of
Heidelberg). For details see e.g. Europhysics Letters 73 (6),
820-825, 2006 or Journal of Chemical Physics 115, No 10,
4829-4838, 2001.
Discrete and Continuous Optimization (1) Dynamical system
approaches to combinatorial optimzation: A dynamical system was
constructed to find feasible solutions of combinatorial optimization
problems (in particular assignment problems). It was proven that the
ω-limit set of the constructed dynamical system is identical to
the set of feasible points of assignment problems. Details can be
found in the chapter J. Starke: "Dynamical System Approaches to
Combinatorial Optimization", Pages 1065-1124 in "Handbook of
Combinatorial Optimization" (Eds. Pardalos, P., Du, D.-Z. and
Graham, R.), 2nd Edition. Springer Verlag, Heidelberg, New
York. 2013.
(2) Iterative procedure to estimate parameter in differential
equations: Joint work with J. Rübel and C. Lux (University of Heidelberg).
For details see
Annals of Operations Research 119,
Special Issue on Optimization in Medicine, 75-100, 2003
and
Journal of Mathematical Biology 51 (2), 157-170, 2005.
(3) Shape optimization with eigenvalue contraints:
This is joint work with
F. Strauß (University of Heidelberg) and M. Inagaki (Toyota CRDL,
Japan). For details see
Structural and Multidisciplinary Optimization 34, 139-149,
2007.
|
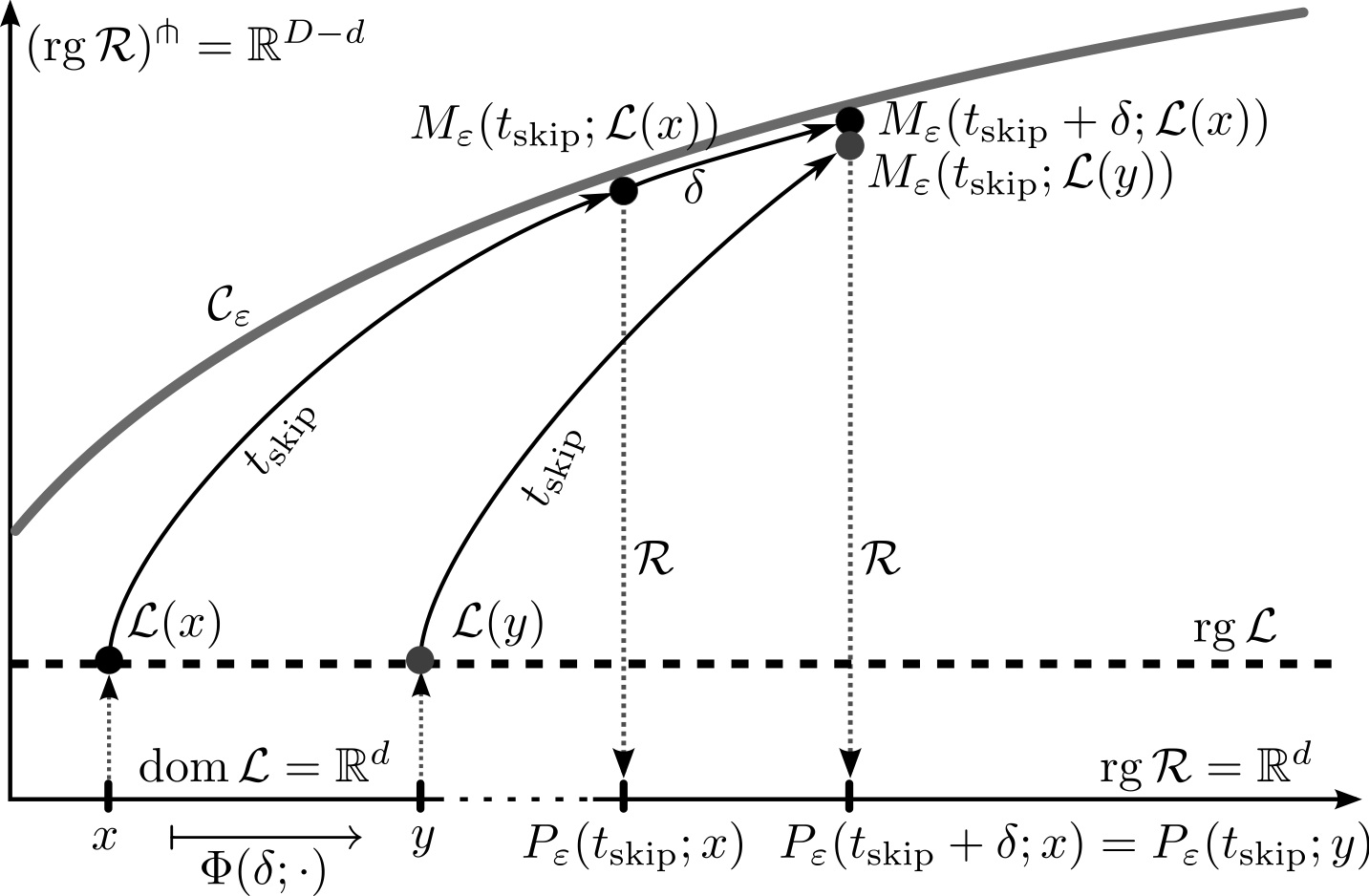 (1) Implicit equation-free methods: In the framework of
equation-free approaches implicit methods were developed which avoid
so-called lifting errors. The equation-free approaches allow to
analyse quantities of interest which live on a macroscopic level even
though no equations are known on that level but only microscopic model
equations. By short simulation bursts of the microscopic model it is
possible to obtain sufficient information for a detailed numerical
analysis of the macroscopic dynamics including continuation techniques
and bifurcation analysis. Error estimates can be given for the
implicit methods. This is joint work with C. Marschler (DTU),
J. Sieber (Exeter, UK), R. Berkemer (AKAD Stuttgart, Germany),
A. Kawamoto (Toyota CRDL, Japan). For details see SIAM Journal on Applied Dynamical Systems (SIADS), 13(3), 1202-1238, 2014.
(1) Implicit equation-free methods: In the framework of
equation-free approaches implicit methods were developed which avoid
so-called lifting errors. The equation-free approaches allow to
analyse quantities of interest which live on a macroscopic level even
though no equations are known on that level but only microscopic model
equations. By short simulation bursts of the microscopic model it is
possible to obtain sufficient information for a detailed numerical
analysis of the macroscopic dynamics including continuation techniques
and bifurcation analysis. Error estimates can be given for the
implicit methods. This is joint work with C. Marschler (DTU),
J. Sieber (Exeter, UK), R. Berkemer (AKAD Stuttgart, Germany),
A. Kawamoto (Toyota CRDL, Japan). For details see SIAM Journal on Applied Dynamical Systems (SIADS), 13(3), 1202-1238, 2014.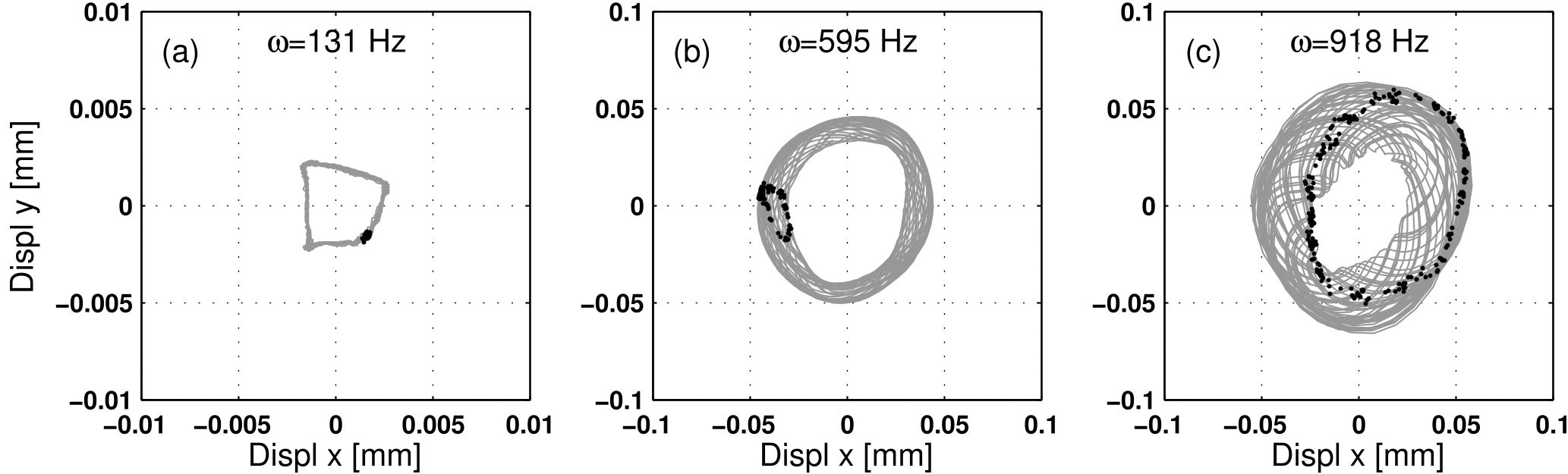 (5) Visualization of Neimark-Sacker bifurcation in experimental
data: Poincare sections visualize a Neimark-Sacker bifurcation in
data from rotating machinery. This
is joint work with F. Schilder (DTU), J. Rübel (University of
Heidelberg), H. Osinga (University of Bristol), B. Krauskopf
(University of Bristol) and M. Inagaki (Toyota CRDL, Japan).
For details see Nonlinear Dynamics 51(4), 529-539, 2008.
(5) Visualization of Neimark-Sacker bifurcation in experimental
data: Poincare sections visualize a Neimark-Sacker bifurcation in
data from rotating machinery. This
is joint work with F. Schilder (DTU), J. Rübel (University of
Heidelberg), H. Osinga (University of Bristol), B. Krauskopf
(University of Bristol) and M. Inagaki (Toyota CRDL, Japan).
For details see Nonlinear Dynamics 51(4), 529-539, 2008.
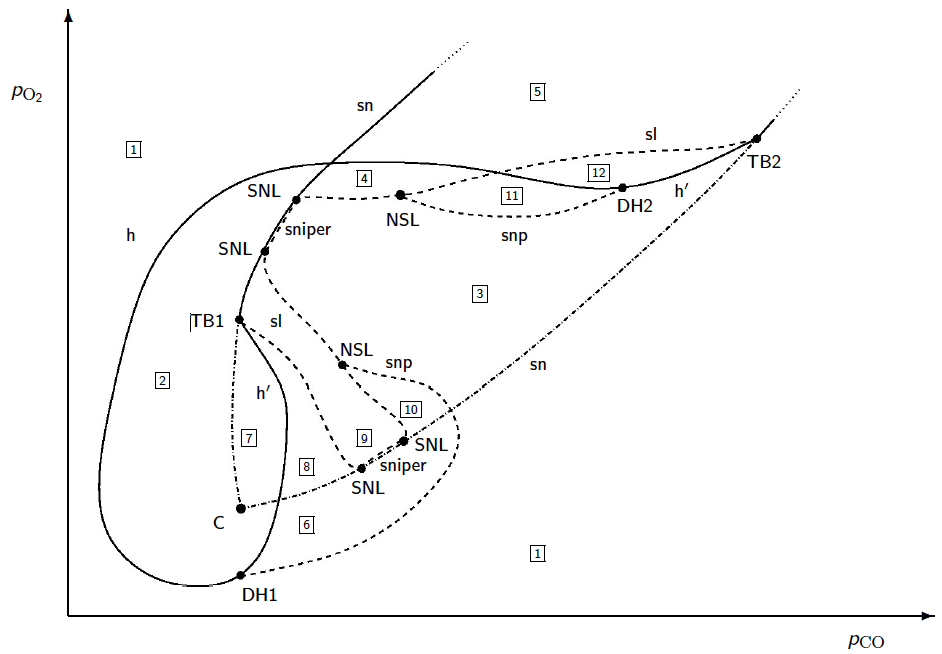 A number of analytical as well as numerical investigations to detect
and continue bifurcation points were performed. This includes the
analysis of the smoothing of a piecewise defined dynamical system,
continuation of tori and an existence proof af a Hopf bifurcation in a
network of bio-chemical reactions. This is in parts joint work with
B. Krauskopf, H. Osinga (Auckland, New Zealand), M. Elmegaard,
F. Schilder, J.J. Thomsen (DTU), O. Corradi and P. Hjorth (DTU),
M. Eiswirth (Fritz Haber Institute Berlin, Germany),
M. Inagaki (Toyota CRDL, Japan). For
details see e.g. SIAM Journal on Applied Dynamical Systems (SIADS),
13(3), 1202-1238, 2014; Journal of
Sound and Vibration 332(22), 5883 - 5897, 2013; SIAM Journal on
Applied Dynamical Systems (SIADS), 11(3), 1007-1032, 2012;
Nonlinear Dynamics 51(4), 529-539, 2008; Journal of Chemical
Physics 115, No 10, 4829 - 4838, 2001.
A number of analytical as well as numerical investigations to detect
and continue bifurcation points were performed. This includes the
analysis of the smoothing of a piecewise defined dynamical system,
continuation of tori and an existence proof af a Hopf bifurcation in a
network of bio-chemical reactions. This is in parts joint work with
B. Krauskopf, H. Osinga (Auckland, New Zealand), M. Elmegaard,
F. Schilder, J.J. Thomsen (DTU), O. Corradi and P. Hjorth (DTU),
M. Eiswirth (Fritz Haber Institute Berlin, Germany),
M. Inagaki (Toyota CRDL, Japan). For
details see e.g. SIAM Journal on Applied Dynamical Systems (SIADS),
13(3), 1202-1238, 2014; Journal of
Sound and Vibration 332(22), 5883 - 5897, 2013; SIAM Journal on
Applied Dynamical Systems (SIADS), 11(3), 1007-1032, 2012;
Nonlinear Dynamics 51(4), 529-539, 2008; Journal of Chemical
Physics 115, No 10, 4829 - 4838, 2001.
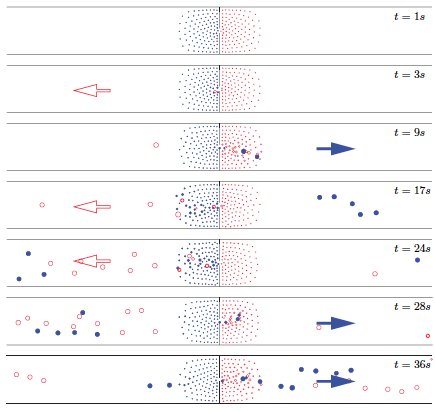 (1) Equation-free analysis of particle models:
The macroscopic behaviour of a microscopically defined particle model
for pedestrian crowds is investigated by equation-free techniques
where no explicitly given equations are available for the macroscopic
quantities of interest. We investigate situations with an intermediate
number of particles where the number of particles is too large for
microscopic investigations of all particles and too small for
analytical investigations using many-particle limits and density
approximations. By developing and combining very robust numerical
algorithms it was possible to perform an equation-free numerical
bifurcation analysis of macroscopic quantities describing the
structure and pattern formation in the particle model. The pedestrian
flow shows the emergence of an oscillatory pattern of two crowds
passing a narrow door in opposite directions. The oscillatory
solutions appear due to a Hopf bifurcation. This is detected
numerically by continuation of a stationary state of the
system. Furthermore, a two-parameter continuation of the Hopf point is
done to investigate the oscillatory behaviour in detail using the door
width and relative velocity of the pedestrians in the two crowds as
parameters.
This is joint work with O. Corradi and P. Hjorth (DTU).
For details see SIAM Journal on Applied Dynamical Systems (SIADS),
11 (3), 1007-1032, 2012.
(1) Equation-free analysis of particle models:
The macroscopic behaviour of a microscopically defined particle model
for pedestrian crowds is investigated by equation-free techniques
where no explicitly given equations are available for the macroscopic
quantities of interest. We investigate situations with an intermediate
number of particles where the number of particles is too large for
microscopic investigations of all particles and too small for
analytical investigations using many-particle limits and density
approximations. By developing and combining very robust numerical
algorithms it was possible to perform an equation-free numerical
bifurcation analysis of macroscopic quantities describing the
structure and pattern formation in the particle model. The pedestrian
flow shows the emergence of an oscillatory pattern of two crowds
passing a narrow door in opposite directions. The oscillatory
solutions appear due to a Hopf bifurcation. This is detected
numerically by continuation of a stationary state of the
system. Furthermore, a two-parameter continuation of the Hopf point is
done to investigate the oscillatory behaviour in detail using the door
width and relative velocity of the pedestrians in the two crowds as
parameters.
This is joint work with O. Corradi and P. Hjorth (DTU).
For details see SIAM Journal on Applied Dynamical Systems (SIADS),
11 (3), 1007-1032, 2012.
 Three levels of modeling, microscopic, mesoscopic and macroscopic are
discussed for the CO oxidation on low-index platinum single crystal
surfaces. The introduced models on the microscopic and mesoscopic
level are stochastic while the model on the macroscopic level is
deterministic. It can be derived rigorously for low-pressure
conditions from the microscopic model, which is characterized as a
moderately interacting many-particle system, in the limit as the
particle number tends to infinity. Also the mesoscopic model is given
by a many-particle system. However, the particles move on a lattice,
such that in contrast to the microscopic model the spatial resolution
is reduced. The derivation of deterministic limit equations is in
correspondence with the successful description of experiments under
low-pressure conditions by deterministic reaction-diffusion equations
while for intermediate pressures phenomena of stochastic origin can be
observed in experiments. The models include a new approach to the
platinum phase transition, which allows for a unification of existing
models for Pt(100) and Pt(110). The rich nonlinear dynamical behavior
of the macroscopic reaction kinetics is investigated and shows good
agreement with low-pressure experiments. Furthermore, for intermediate
pressures, noise-induced pattern formation, which has not been
captured by earlier models, can be reproduced in stochastic
simulations with the mesoscopic model. This is joint work with
M. Eiswirth, H. Rotermund, G. Ertl (Frith Haber Institut, Berlin),
K. Oelschlaeger (University of Heidelberg) and C. Reichert (University
of Heidelberg). For details see e.g.
Europhysics Letters 73 (6), 820-825, 2006
or
Journal of Chemical Physics 115, No 10, 4829-4838, 2001.
Three levels of modeling, microscopic, mesoscopic and macroscopic are
discussed for the CO oxidation on low-index platinum single crystal
surfaces. The introduced models on the microscopic and mesoscopic
level are stochastic while the model on the macroscopic level is
deterministic. It can be derived rigorously for low-pressure
conditions from the microscopic model, which is characterized as a
moderately interacting many-particle system, in the limit as the
particle number tends to infinity. Also the mesoscopic model is given
by a many-particle system. However, the particles move on a lattice,
such that in contrast to the microscopic model the spatial resolution
is reduced. The derivation of deterministic limit equations is in
correspondence with the successful description of experiments under
low-pressure conditions by deterministic reaction-diffusion equations
while for intermediate pressures phenomena of stochastic origin can be
observed in experiments. The models include a new approach to the
platinum phase transition, which allows for a unification of existing
models for Pt(100) and Pt(110). The rich nonlinear dynamical behavior
of the macroscopic reaction kinetics is investigated and shows good
agreement with low-pressure experiments. Furthermore, for intermediate
pressures, noise-induced pattern formation, which has not been
captured by earlier models, can be reproduced in stochastic
simulations with the mesoscopic model. This is joint work with
M. Eiswirth, H. Rotermund, G. Ertl (Frith Haber Institut, Berlin),
K. Oelschlaeger (University of Heidelberg) and C. Reichert (University
of Heidelberg). For details see e.g.
Europhysics Letters 73 (6), 820-825, 2006
or
Journal of Chemical Physics 115, No 10, 4829-4838, 2001.
 (2) Modeling of axonal pathfinding in the olfactory system - sorting
and convergence: Models with attracting and repulsive interactions
were proposed which are able to reproduce the experimental findings of
sorting and convergence during axonal pathfinding in the olfactory
system. Many axon species, each represented by a huge number of axons,
are spatially disordered at the beginning of their growth at the
receptor neurons and converge by a self-organized process to a sorted
state, i.e. axons of the same receptor type converge to a common
position. Under certain model assumptions, it can be proved that the
interacting many-particle system of different particle types converges
to a sorted state. This is joint work with S. Kokkendorff (DTU),
J. Strotmann (University of Hohenheim), N. Hummel (University of
Heidelberg). For details see SIAM Journal on Applied Mathematics (SIAP)
70(7), 2534-2555, 2010.
(2) Modeling of axonal pathfinding in the olfactory system - sorting
and convergence: Models with attracting and repulsive interactions
were proposed which are able to reproduce the experimental findings of
sorting and convergence during axonal pathfinding in the olfactory
system. Many axon species, each represented by a huge number of axons,
are spatially disordered at the beginning of their growth at the
receptor neurons and converge by a self-organized process to a sorted
state, i.e. axons of the same receptor type converge to a common
position. Under certain model assumptions, it can be proved that the
interacting many-particle system of different particle types converges
to a sorted state. This is joint work with S. Kokkendorff (DTU),
J. Strotmann (University of Hohenheim), N. Hummel (University of
Heidelberg). For details see SIAM Journal on Applied Mathematics (SIAP)
70(7), 2534-2555, 2010.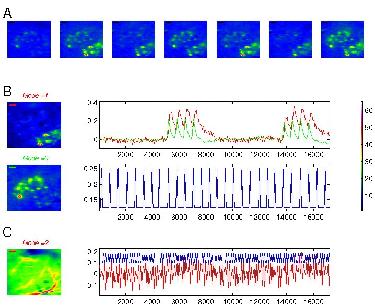 (3) Spatio-temporal dynamics in the olfactory bulb: Odors evoke a
variety of stimulus specific spatio-temporal patterns on the levels of
glomeruli and neural network of mitral and granular cells in the
olfactory bulb which can be measured for mice in vivo using Ca and
voltage sensitive dyes for optical imaging. A spatial independent
component analysis (sICA) of this high-resolution imaging data was
used to separate different neuronal populations based on their
stimulus specific spatio-temporal activation. They can be identified
as groups of glomeruli with different response latencies. Artifacts
due to movement, heartbeat or respiration are automatically separated
from the functional signal by sICA. Other applications were the
somatosensory cortex of mice as well as the visual cortex of
monkeys. Equation-free techniques allow for a systematic analysis of
macroscopic network activities and their dependence on biological
parameters such as kinetic parameters or network topology. This is
joint work with C. Ellsaesser, T. Kuner and J. Reidl (University of
Heidelberg), J. Midtgaard (University of Copenhagen),
D. Omer, A. Grinvald (Weizmann Institute of Science) and
H. Spors (Max Planck Institute for medical research, Heidelberg).
For details see e.g. NeuroImage 34, 94-108, 2007.
(3) Spatio-temporal dynamics in the olfactory bulb: Odors evoke a
variety of stimulus specific spatio-temporal patterns on the levels of
glomeruli and neural network of mitral and granular cells in the
olfactory bulb which can be measured for mice in vivo using Ca and
voltage sensitive dyes for optical imaging. A spatial independent
component analysis (sICA) of this high-resolution imaging data was
used to separate different neuronal populations based on their
stimulus specific spatio-temporal activation. They can be identified
as groups of glomeruli with different response latencies. Artifacts
due to movement, heartbeat or respiration are automatically separated
from the functional signal by sICA. Other applications were the
somatosensory cortex of mice as well as the visual cortex of
monkeys. Equation-free techniques allow for a systematic analysis of
macroscopic network activities and their dependence on biological
parameters such as kinetic parameters or network topology. This is
joint work with C. Ellsaesser, T. Kuner and J. Reidl (University of
Heidelberg), J. Midtgaard (University of Copenhagen),
D. Omer, A. Grinvald (Weizmann Institute of Science) and
H. Spors (Max Planck Institute for medical research, Heidelberg).
For details see e.g. NeuroImage 34, 94-108, 2007.
 (2) Traffic jam control:
It is shown that a deterministic as well as a stochastic modulation
of the safety distance can extend the stability region of the
uniform flow and therefore reduce traffic jams.
This is a collaboration with Y. Gaididei
(Kiev, Ukraine), R. Berkemer (DTU), P. L. Christiansen (DTU),
A. Kawamoto & T. Shiga (Toyota CRDL, Japan) and M.P. Sørensen
(DTU). For details see NHM (Networks and Heterogeneous Media)
8(1), 261-273, 2013, and
Physical Review E 88(4), 042803 - 042815, 2013.
(2) Traffic jam control:
It is shown that a deterministic as well as a stochastic modulation
of the safety distance can extend the stability region of the
uniform flow and therefore reduce traffic jams.
This is a collaboration with Y. Gaididei
(Kiev, Ukraine), R. Berkemer (DTU), P. L. Christiansen (DTU),
A. Kawamoto & T. Shiga (Toyota CRDL, Japan) and M.P. Sørensen
(DTU). For details see NHM (Networks and Heterogeneous Media)
8(1), 261-273, 2013, and
Physical Review E 88(4), 042803 - 042815, 2013.
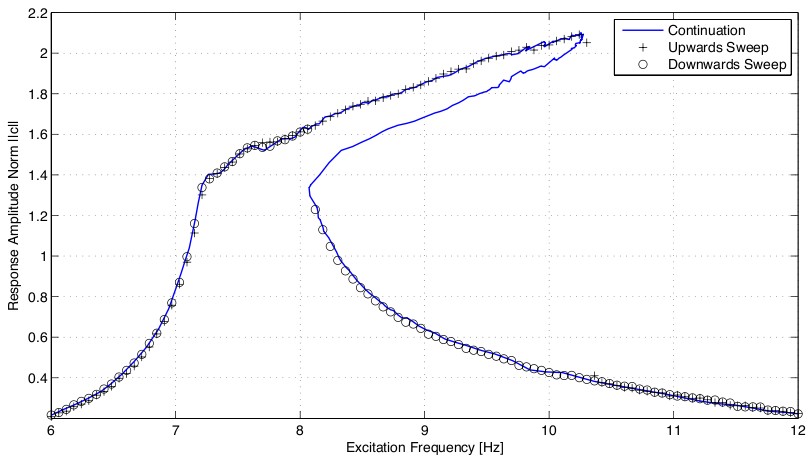
 (1) Continuation and bifurcation analysis of experiments:
Applying continuation methods directly to a controlled lab experiment
allows to obtain valuable experimental information which is important
for model development and verification. By this, it is
possible to systematically explore how stable and unstable steady
state periodic vibrations depend on parameters. The approach is tested
on a driven mechanical oscillator with a strong impact nonlinearity,
controlled with electromagnetic actuators.
The controller is tuned
such that the steady state dynamics of the controlled experiment
matches that of the corresponding un-controlled experiment. The figure
shows an experimentally obtained bifurcation diagram (amplitude over
driving frequency) including the unstable branch. This is joint work
with F. Schilder, E. Bureau, I. Santos and J.J. Thomsen (DTU).
For details see
Proceedings of ENOC Conference, 24-29 July 2011, Rome, Italy;
Journal of Sound and Vibration 332(22), 5883-5897,
2013 & Journal of Sound and Vibration 333(21), 5464-5474, 2014.
(1) Continuation and bifurcation analysis of experiments:
Applying continuation methods directly to a controlled lab experiment
allows to obtain valuable experimental information which is important
for model development and verification. By this, it is
possible to systematically explore how stable and unstable steady
state periodic vibrations depend on parameters. The approach is tested
on a driven mechanical oscillator with a strong impact nonlinearity,
controlled with electromagnetic actuators.
The controller is tuned
such that the steady state dynamics of the controlled experiment
matches that of the corresponding un-controlled experiment. The figure
shows an experimentally obtained bifurcation diagram (amplitude over
driving frequency) including the unstable branch. This is joint work
with F. Schilder, E. Bureau, I. Santos and J.J. Thomsen (DTU).
For details see
Proceedings of ENOC Conference, 24-29 July 2011, Rome, Italy;
Journal of Sound and Vibration 332(22), 5883-5897,
2013 & Journal of Sound and Vibration 333(21), 5464-5474, 2014.
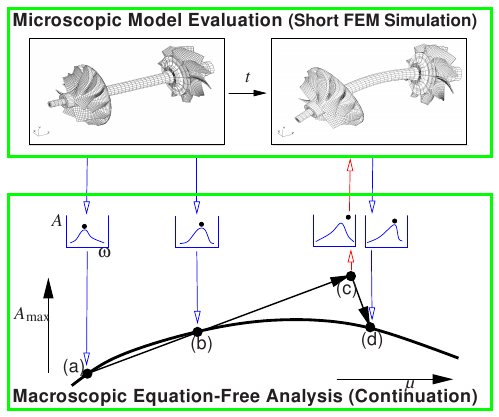 (4) Analysis of rotating machinery:
Efficient computation of quasiperiodic oscillations
in nonlinear systems with fast rotating parts
We present a numerical method for the investigation of quasiperiodic
oscillations in applications modeled by systems of ordinary
differential equations. An important element of our approach is that
it allows us to verify whether one can neglect gravitational forces
after a change of coordinates into a corotating frame. Specifically,
we show that this leads to a dramatic reduction of computational
effort. A turbocharger model is studied as a practical example. This
is joint work with F. Schilder (DTU), J. Rübel (University of
Heidelberg), H. Osinga (University of Bristol), B. Krauskopf
(University of Bristol) and M. Inagaki (Toyota CRDL, Japan).
For details see Nonlinear Dynamics 51(4), 529-539, 2008 and
DETC2009-87339, Proc. of the ASME 2009 International Design
Engineering Technical Conferences & Computers and Information in
Engineering Conference, IDETC/CIE 2009.
(4) Analysis of rotating machinery:
Efficient computation of quasiperiodic oscillations
in nonlinear systems with fast rotating parts
We present a numerical method for the investigation of quasiperiodic
oscillations in applications modeled by systems of ordinary
differential equations. An important element of our approach is that
it allows us to verify whether one can neglect gravitational forces
after a change of coordinates into a corotating frame. Specifically,
we show that this leads to a dramatic reduction of computational
effort. A turbocharger model is studied as a practical example. This
is joint work with F. Schilder (DTU), J. Rübel (University of
Heidelberg), H. Osinga (University of Bristol), B. Krauskopf
(University of Bristol) and M. Inagaki (Toyota CRDL, Japan).
For details see Nonlinear Dynamics 51(4), 529-539, 2008 and
DETC2009-87339, Proc. of the ASME 2009 International Design
Engineering Technical Conferences & Computers and Information in
Engineering Conference, IDETC/CIE 2009.
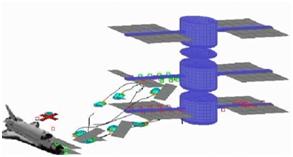 Time-dependent robot-target assignment problems with several
autonomous robots and several targets are considered as model of
flexible manufacturing systems. Each manufacturing target has to be
served in a given time interval by one and only one robot and the
total working costs have to be minimized (or total winnings
maximized). A specifically constructed dynamical system approach
(coupled selection equations) is used which guarantees feasiblitiy of
the assignment solutions. This type of control is based on pattern
formation principles known in physics, chemistry and biology and
results in fault resistant and robust behaviour. The performance of
the suggested control is demonstrated and visualized with a computer
simulation of autonomous space robots building a space station by
distributed transporting several parts from a space shuttle to defined
positions at the space station. This is in parts joint work with
C. Ellsaesser, University of Heidelberg, T. Fukuda (Nagoya University),
H. Haken (University of Stuttgart), P. Molnar (Clark Atlanta University)
and M. Schanz (University of Stuttgart).
For details see e.g.
Physics Letters A 375, 2094-2098, 2011;
The International Journal of Robotics Research 24,
465 - 486, 2005;
IEEE Transactions on
Systems, Men and Cybernetics: Part B, 31, No. 3, 433-436,
2001.
Time-dependent robot-target assignment problems with several
autonomous robots and several targets are considered as model of
flexible manufacturing systems. Each manufacturing target has to be
served in a given time interval by one and only one robot and the
total working costs have to be minimized (or total winnings
maximized). A specifically constructed dynamical system approach
(coupled selection equations) is used which guarantees feasiblitiy of
the assignment solutions. This type of control is based on pattern
formation principles known in physics, chemistry and biology and
results in fault resistant and robust behaviour. The performance of
the suggested control is demonstrated and visualized with a computer
simulation of autonomous space robots building a space station by
distributed transporting several parts from a space shuttle to defined
positions at the space station. This is in parts joint work with
C. Ellsaesser, University of Heidelberg, T. Fukuda (Nagoya University),
H. Haken (University of Stuttgart), P. Molnar (Clark Atlanta University)
and M. Schanz (University of Stuttgart).
For details see e.g.
Physics Letters A 375, 2094-2098, 2011;
The International Journal of Robotics Research 24,
465 - 486, 2005;
IEEE Transactions on
Systems, Men and Cybernetics: Part B, 31, No. 3, 433-436,
2001.
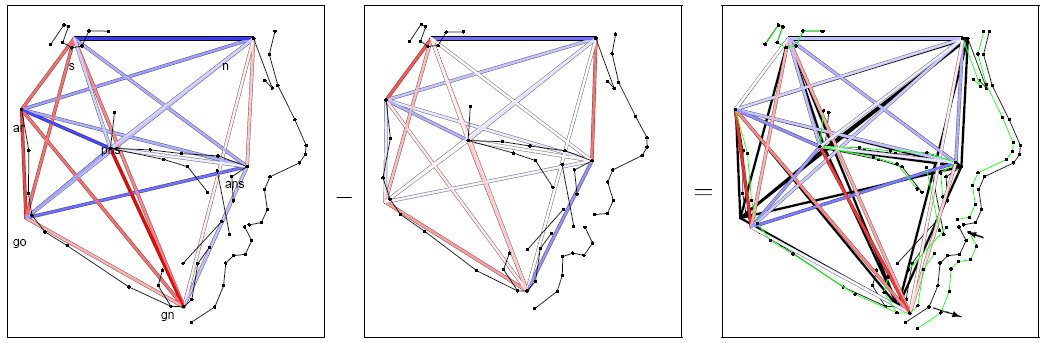 (1) Modelling of the growth dynamics: Decomposing orthodontic
growth data in spatial growth modes by an adapted Karhunen-Loeve
decomposition allows for a substantial dimension reduction and a
subsequential modelling. The complex nonlinearly coupled growth
regions can therefore be described by a low-dimensional dynamics with
time-independent modes. The obtained dynamical system description can
be used to predict future shape changes.
(1) Modelling of the growth dynamics: Decomposing orthodontic
growth data in spatial growth modes by an adapted Karhunen-Loeve
decomposition allows for a substantial dimension reduction and a
subsequential modelling. The complex nonlinearly coupled growth
regions can therefore be described by a low-dimensional dynamics with
time-independent modes. The obtained dynamical system description can
be used to predict future shape changes.